Here is a sampling of talks that I have given.
Integrating community assembly into modern coexistence theory: Understanding the mechanisms allowing interacting populations to co-occur underlies many questions in ecology, evolution, and epidemiology. One widely used metric for understanding coexistence are invasion growth rates: the average per-capita growth rates of populations when rare. These invasion growth rates are the basis of Modern Coexistence Theory (MCT). Currently, this theory assumes coexistence occurs when each species, say species i, has a positive invasion growth rate in the community determined by its absence, so called -i communities. Intuitively, coexistence occurs if each species can recover from being rare. However, there are well known examples where this heuristic fails. Moreover, even if this heuristic applies, it isn’t always clear what is meant by -i communities. To address these issues, Josef Hofbauer and I introduced a broadly applicable mathematical theory that answers two questions (i) when do the signs of the invasion growth rates determine coexistence? (ii) When the signs are sufficient, which invasion growth rates need to be positive? These slides are from a talk that I gave at ESA in Montreal (2022). I also gave longer, more mathematical versions of this talk at the sectional AMS meeting in Salt Lake City (2022) and the Joint Mathematics Meetings in Boston (2023). These talks are based on this paper in the Journal of Mathematical Biology.
Coevolution of patch-selection in the face of environmental stochasticity: Species interact in landscapes where environmental conditions vary in time and space. To understand how this variability impacts habitat choice, Alex Hening, Dang Nguyen, and I analyzed coevolutionarly stable strategies for habitat choice in spatially implicit Lotka-Volterra models accounting for environmental stochasticity. In occupied patches at the coESS, we show that the differences between the local contributions to the mean and the variance of the long-term population growth rate are equalized. Applying this characterization to models of antagonistic interactions reveals that environmental stochasticity can partially exorcize the ghost of competition past, select for new forms of enemy-free and victimless space, and generate Hydra effects over evolutionary time scales. Viewing our results through the economic lens of Modern Portfolio Theory highlights why the coESS for patch selection is often a bet-hedging strategy coupling stochastic sink populations. Our results highlight how environmental stochasticity can reverse or amplify evolutionary outcomes due to species interactions or spatial heterogeneity. The slides (part 1, part 2, part 3) are from a talk that I gave at the Institut Henri Poincaré in 2022.
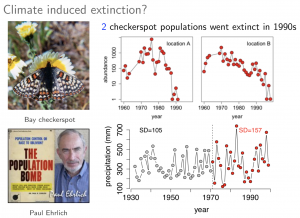Stochastic persistence and extinction: Two long standing, fundamental questions in biology are “Under what conditions do populations persist or go extinct? When do interacting species coexist?” The answers to these questions are essential for guiding conservation efforts and identifying mechanisms that maintain biodiversity. Mathematical models play an important role in identifying these mechanisms and, when coupled with empirical work, can determine whether or not a given mechanism is operating in a specific population or community. For over a century, nonlinear difference and differential equations have been used to identify these mechanisms. These models, however, fail to account for stochastic fluctuations in environmental conditions such as temperature and precipitation. In this talk, I present theorems about persistence, coexistence, and extinction for stochastic difference equations that account for species interactions, population structure, and environmental fluctuations. The theorems are illustrated with models of Bay checkerspot butterflies, spatially structured acorn woodpecker populations, competition among annual plants, evolutionary games of and rock-paper-scissor. These slides are from a talk that I gave at Shanghai Normal University, Fudan University, Harbin Engineering University, an Renmin University during a 2019 trip to China . I have given variants of this talk at at the Neyman Seminar in UC/Berkeley, CIRM in France, IMA at University of Minnesota, University of Alberta, the BAMM conference in Richmond, VA, and the University of Pennsylvania.